57

57. Вывод уравнения Гиббса-Дюгема. Их применение к расчету термодинамических свойств.

Если раствор находится при постоянных Т и Р, то его экстенсивное свойство будет зависеть только от состава раствора:

g=f(n₁, n₂, n₃,…, n_k)

Тогда

Или , (1)

Где dg-изменение экстенсивного свойства раствора при добавлении к нему dn₁ молей 1-го компонента, dn₂ молей 2-го компонента и т.д. небольшими порциями и в таком соотношении, чтобы состав раствора не изменялся. При таком добавлении изменится масса раствора, а парциальные молярные величины останутся неизменными.

Величину экстенсивного свойства раствора находим, проинтегрировав уравнение (1).

Уравнение Гиббса-Дюгема

Постоянная интегрирования в уравнении равна нулю, т.к. при всех n_i=0 g=0.

Если в качестве экстенсивного раствора взять объем, то уравнение Гиббса –Дюгема выглядит таким образом: , где V-общий объем раствора. Аналогично, при постоянстве состава раствора можно через парциальные молярные величины выразить другие экстенсивные свойства(внутренняя энергия, энтропия итд)

Если одновременно изменяются и состав раствора. и его количество. То при дифференцировании уравнения Гиббса-Дюгема получаем общее изменение экстенсивного свойства.

(2)

Если приравнять (1) и (2),получаем второе уравнение Гиббса-Дюгема:

Это уравнение можно записать в другой форме, если обе его части поделить на

∑n_i=n₁+n₂+…+n_k

Где х₁, х₂…х_к-молярные доли действующих компонентов раствора

58. Понятие об активности и коэффициенте активности. Симметричная и несимметричная нормировка стандартного состояния.

Уравнения, выведенные для идеальных растворов, оказались непригодными для описания свойств реальных растворов. Поэтому сохранили форму выведения уравнений для реальных растворов, заменив в них концентрацию на активность (а). Уравнение химического потенциала выглядит так:

Значение μ⁰_i_,_xв уравнениях для химически потенциалов в растворе и чистом растворителе одинаковы. поэтому при вычитании получаем:

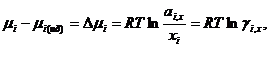т.е -коэффициент активности.

Подставляем в известное термодинамическое соотношение ∆G=-W (W-максимальная полезная работа) и учитывая соотношение 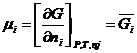,находим

, отсюда

Следовательно, коэффициент активности характеризует работу, которую нужно затратить для переноса 1 моль вещества из идеального в реальный раствор той же концентрации. Эта работа затрачивается на преодоление сил, вызывающих отклонение свойств реального раствора от свойств идеального.

Числовое значение коэф. активности зависит от способа выражения концентрации раствора.

, а_i_,_x-активность i-го компонента в растворе, концент. кот выражена в молярных долях (х_i);γ_i_,_x-рациональный коэф.активности.

, а_i_,_m-активность i-го компонента в растворе, концент. кот выражена ч/з моляльность (m_i);γ_i_,_m-моляльный или практический коэф. активности

. а_i_,С-активность i-го компонента в растворе, концент. кот выражена ч/з молярность (С_i);γ_i_,С-молярный коэф. активности

Связь коэф.активности между различными способами выражениями

, М₁-молярная масса рас-ля.

В симметричной системе за стандартное состояние каждого компонента раствора принимается состояние чистого вещества. когда раствор образуется из жидких компонентов. Активность (а⁰_i) каждого компонента принимается равной единице. Симметричная система стандартного состояния применяется при изучении растворов неэлектролитов.

В несимметричной системе стандартным состоянием растворителя остается его состояние чистого вещества с активностью растворителя в стандартном состоянии, равной единице.

59. Основные виды растворов неэлектролитов и электролитов. Влияние различных факторов на растворимость твердых тел.

Раствор- однородная смесь, состоящая из 2-х или большего числа веществ, состав которой в определенных пределах может непрерывно изменяться .

Жидкие раствор. В жидких рас-рах обычно различают растворитель и растворенное вещество.но это деление крайне условное. Под растворителем понимают веществово, которое имеется в растворе в большем количестве, а остальные компоненты присутствующие в меньших количествах, называются растворенными веществами.

При образовании жидких растворов растворенное вещ-во может находиться в виде отдельных молекул или ассоциатов, состоящих из нескольких молекул, либо частично или полностью диссоциировать на ионы. В связи с этим жидкие растворы подразделяются на электролиты и неэлктролиты.

Растворы тв. тел в жидкостях называют истинными если они гомогенны т/д-ки устойчивы.

Характеристики истинных растворов

- минимальная энергия Гельмгольца ∆А или энергия Гиббса ∆G

-максимальная энтропия ∆S

Классификация по количеству растворенного вещества

▪ ненасыщенные (содержание вещества в р-ре меньше равновесного, осадок в системе отсутствует);

▪насыщенный (содержит такое кол-во вещ-ва, кот. находится в равновесии с осадком на дне сосуда(донная фаза);

▪ пересыщенные (при отсутствии центров кристаллизации в жидкости можно растворить вещ-во в количестве превышающем равновесное).Растворы т/д-ки неустойчивы, т.к упругость пара пересыщенного р-ра выше, чем над насыщенными(равновесными) при Т=соnst. Перенасыщенные рас-ры можно получить при быстром охлаждении ненасыщенного р-ра до температуры при кот. Создается перенасыщение. Существование перенасыщ. р-ров связано с тем, что субмикрокристаллы имеют повышен. Растворимость, т.к. они обладают повышенной упругостью насыщенного пара. Поэтому они растворяются и это затрудняет кристаллизацию вещ-ва из перенасыщ. раствора.Перенасыщ р-ры метастабильны, но со временем переходят в стабильное состояния, засчет выпадения осадка.Это процесс облегчится путем введенич центров кристаллизации(пылинки, флуктуация концентраций)

= Равновесные концентрации завсят от Т и Р, природы р-ля и рас-го вещ-ва.

Равновесие в гетерогенной системе жид.-тв. является динамичным и характеризуется

υ _{осаждения}=υ _{растворения}

Влияние различных факторов на растворимость тв. тел в жидкостях.

- природа. Полярные вещества растворяются в полярных, неполярные в неполярных.

А в смешанных р-рах смотрим на соотношение веществ, т.е чего больше полярного или неполярного.

-температура. Процесс растворение сопровождается выделением и поглощением теплоты, кот можно представить в виде суммы теплоты плавления (эндопроцесс) и сольватации (экзопроцесс).

∆H^p=∆H_T^пл+∆H_T^сольв ∆Н^р<>=0

В зависимости от знака ∆Н^ри ее величины ↑ температуры по-разному влияет на растворимость. Р-ть солей резко ↑ с ↑ Т (пример KNO₃).Р-ть мелких кристаллов выше чем крупных.

60. Уравнение расчета растворимости твердых тел в жидкости как функция температуры.

Рассмотрим систему раствор и донная фаза которые находятся в равновесии при постоянстве давления и температуры.

Вычитаем

Дифференцируем по температуре

(1)

Химический потенциал растворенного вещества для идеальных растворов

Дифференцируем по х₂

₍₂₎

Раскрываем сущность производных μ_2Ни μ_2Тпо Т в таком виде:

(3)

(4)

Подставляем 2, 3, 4 в 1, после деления на дТ получим

Подставим это выражение в уравнение, и получим уравнение Шредера для идеальных растворов

Чтобы это уравнение стало справедливым для реальных растворов заменим х₂на а₂ –активность. Теплота в этом случае будет полной теплотой растворения, получаемой при растворении 1 моля вещества в таком количестве раствора, чтобы был получен насыщенный раствор.

Зависимость активности от температуры

Если ∆Н^р>0, то (дlna₂/дT)_p>0 b c ↑ T растворимость растет

Если ∆Н^р=0, то (дlna₂/дT)_p=0 b c ↑ T растворимость не изменяется

61. Уравнение зависимости растворимости твердых тел от давления.

Для равновесного состояния справедливо равенство

(*),

μ_2Н, μ_2ТВ-химический потенциал вещества в растворе и донной фазе.

При изменении давления на dP изменится на дифференциально малую величину и химический потенциал, но равновесие в системе при Т=соnst снова установится через некоторое время.

Дифференцируем (*) по х₂и р

(1)

Химический потенциал растворенного вещества для ид. растворов

Дифференцируем по х₂

₍₂₎

Раскрываем сущность производных μ_2Ни μ_2Тпо Т в таком виде:

(3)

(4)

где , -порциальный мольный объем растворенного вещества в растворе и донной фазе.

Подставляем 2,3.4 в 1,после деления на дТ получим

Разность есть прирост объема раствора при его создании, но т.к эта величина незначительна и влияние давления на растворимость твердых тел невелико.

Для большинства веществ , следовательно с ростом давления растворимость твердых веществ в жидкостях должна уменьшаться.

62. Закон Рауля. Аналитическое выражение, физический смысл понижения давления насыщенных паров над раствором. Следствие из закона Рауля.

Для разбавленных р-ров неэлектролитов давление насыщенного пара жидкости снижается прямо пропорционально концентрации растворенного вещества. Такие растворы называются идеальными.

Для разбавленных растворов неэлектролитов давление пара растворителя над раствором снижается с повышением мольной доли его в растворе:

р_А=р⁰_Ах₁, закон Рауля

где р_А, р⁰_А-давление пара растворителя над раствором и над чистым растворителем;

х₁-мольная доля растворителя.

В бинарной смеси вещества х₁+х₂=1 => х₁=1-х₂

р⁰-р=р⁰-р⁰х₁

Этот закон выполняется если:

-пар при ↑Т пара не является идеальным, поэтому нужно вводить коэффициент фугитивности.

f_i= f⁰_ix₂

-при ↑р в р-ре жидкостей для 2-го компонента справаведлив закон Генри :

х₂=k ∙p_Bк-константа Генри

если паровая фаза обладает идеальными свойствами, тогда

к=I/p⁰_B

и закон Генри записывается в такой форме:

p_B=p⁰_Bх₂

Физический смысл понижения давления насыщенных паров над раствором.

=над раствором давление насыщ. пара ниже чем над чистым р-лем. Это объясняется различием объемных и поверхностных свойств раствора. Молекулы находящиеся в объеме жидкости испытывают одинаковые ММВ со стороны молекул координационных сфер. Поэтому любое перемещение равновероятно и не требует затраты работы. Молекулы со стороны жидкости имеют оч.большое притяжение внутренних слоев – это называется внутренним давлением(а/υ²).Чтобы молекулы перешли в паровую фазу нужно υ_исп> υ _конд;Е_к > а/RT

В гетерогенных системах давление насыщ пара зависит :

- от природы жидкости

- температуры

-кривизны поверхности

При растворении тв. тела в жидкости создаются смешанные полиэдры, что снижает число молекул растворителя уходящих в паровую фазу .Чем больше растворенного вещества, тем ↑ разница понижения давления.

63. Диаграмм состояния воды и водного раствора электролита и неэлектролита.

Поле этой диаграммы для чистой воды разделяется кривыми ОА, ОВ и ОС на три области, отражающие отражающие гомогенные системы. Кривая ОА характеризует равновесие в системе жидкость-пар

(f=1-2+2=1), ОВ - лед-жидкость (f=1), ОС - лед-пар (f=1). В точке 0 система трехфазна и имеет нулевое число степеней свободы

f=1-3+2=0.Кривые ОА, ОВ и ОС описываются уравнениями Клаузиуса-Клапейронав таком виде.

где ∆Н_Т– теплоты фазовых переходов,

υ_Г,υ_Ж,υ_Т–мольные обемы.

Кривая ОВ располагается под отрицательным углом наклона, так как υ_Ж<υ_ТВ.

Растворение неэлектролитов в воде (сахар) снижает давление насыщенного пара над раствором при всех температурах (см. кривую О₁А₁)

Для определения температуры кипения чистой воды и раствора проведем изобару внешнего давления Р^внеш. Тогда точка а₁ определяет Т_кип чистой воды, а точка а₂- Т_кип раствора. Известно что жидкость закипает когда внутреннее давление жидкости равно внешнему давлению. Из рис. Видно , что ∆Р_нас над раствором ниже, чем над чистой водой на величину ∆Р, поэтому для закипания раствора и для выравнивания давления над раствором с внешним давлением нужно повысить температуру до Т_к.

Растворитель замерзает при условии, что давление над жидкостью становиться равным давлению над льдом. Этому условию соответствует точка 0. Над раствором давление ниже, чем над чистой жидкостью на ∆Р. Раствор замерзает, когда давление над ним равно давлению над льдом в растворе. Этому условию соответствует точка О₁. Из рис. 40 следует, что раствор замерзает при более низкой температуре, чем чистая вода.

64. Термодинамический вывод уравнения закона Рауля .

При равновесии химический потенциал вещества одинаков во всех существующих фазах. Очевидно, хим. Потенциал компонента жидкого раствора μ_i_(Ж) будет равен химическому потенциалу пара этого компонента μ_i_(П) над раствором:

μ_i_(Ж)= μ_i_(П)

Подставляем уравнения химических потенциалов идеальных растворов

= (1)

Давление пара вещества над чистым растворителем равно Р⁰_i, поэтому при х_i=1 (чистое вещество) уравнение переходит в

= (2)

Подстановка соотношения (2) в (1) дает

Откуда после небольших упрощений получается уравнение р₁=р⁰₁х₁

Если раствор состоит из 2-х летучих компонентов. А пар обладает свойствами идеального газа, то закон Рауля будет справедлив как для р-ля, так и для растворенного вещества: р₁=р⁰₁х₁(3)

Р₂=р⁰₂х₂ (4)

Общее давление равно сумме парциальных давлений пара отдельных компонентов:

Р=Р⁰₂+(Р⁰₁-Р⁰₂)х₁ (5)

Из уравнений 3-5 следует, что парциальные давления пара р-ля и растворенного вещества, а также общее давление пара над идеальным раствором линейно зависят от состава раствора.